Graphs Adjacency Lists

http://sourcecodemania.com/graph-implementation-in-cpp/  for details on implementation in C++.

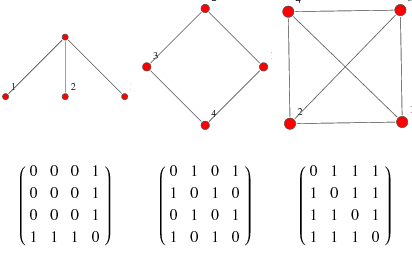
An issue that you man encounter when dealing with graphs sparsity.  There are a lot of case where you create an adjacency matrix to hold your data and realize it is full of 0s.  That can or cannot be useful depending on your application.  Be for a more space efficient data structure use the Adjacency list (diagram above).  The basic idea here is to create N x 1 array of linked lists.  The elements in the linked list represent the connection the head node (node in graph) is connected to. Example from diagram above, Note that a is connected to d, b, c.  Look up a in the array and note that a's linked list has all of its connections.

Graph to Adjancency Matrix

Graph Structures

I have always wondered how to represent Graphs when programming.  The answer came in the form of a Adjancy Matrix.  This is a incredibly neat way to store all the nodes and represent the edges between two nodes.

Below is a diagram of how it works:

Essentially, rows and columns represent the node 1..4 (from right to left) and 1..4  (up and down).  Everytime you have a connection you flip the bit in the matrix to 1 from 0.  So there is a path from 1 to 4 the data point at M(1,4) and M(4,1) will be 1.

Red Black Trees

So, you can get screwed if you have to construct (insert operation) based on Sorted Data.  You can get a highly unbalanced tree.  How to solve this??

Awesome explanation taken from SO( original post ) :

Red Black trees are good for creating well-balanced trees. The major problem with binary search trees is that you can make them unbalanced very easily. Imagine your first number is a 15. Then all the numbers after that are increasingly smaller than 15. You'll have a tree that is very heavy on the left side and has nothing on the right side.

Red Black trees solve that by forcing your tree to be balanced whenever you insert or delete. It accomplishes this through a series of rotations between ancestor nodes and child nodes. The algorithm is actually pretty straightforward, although it is a bit long.

The implementation is also not really so short so it's probably not really best to include it here. Nevertheless, trees are used extensively for high performance apps that need access to lots of data. They provide a very efficient way of finding nodes, with a relatively small overhead of insertion/deletion. 

While BSTs may not be used explicitly - one example of the use of trees in general are in almost every single modern RDBMS. Similarly, your file system is almost certainly represented as some sort of tree structure, and files are likewise indexed that way. Trees power Google. Trees power just about every website on the internet.

BackTracking

The simplest explanation of this technique just sunk in for me so I thought I would put it up before I completely forget it.

So, it works like this....

Think about having to go down a decision tree (a highly branched tree.

Now there are a few possible answers and they are at the leaf level.  And imagine you are starting at the root level.

So, the way you would "backtrack" is to start down a branch (branch picking to start the problem is a bit beyond me).  But you would continue down from one branch to another until you get to the leaf (most examples I saw do this recursively).  If the leaf is the solution you are done!  If not, you will back up, I think of rewinding, back to the original position and trying down another branch.   

Now obviously this is a super simple understanding of a complex technique.  Things that should be given some more thought include keeping track of position so that you do go down a failed route again and again.   

PPT of BackTracking << Helped me in getting a better idea of how this works.

String Matching with Hash

Pretty clever algorithm that illustrates doing this with hash:

Rabin-Karp
http://en.wikipedia.org/wiki/Rabin%E2%80%93Karp_algorithm

But worse case scenario, not likely to happen, is that every hash collides and then you have a quadratic time.

Selecting a datastructure

When faced with selecting a data structure:

Look at the operations to perform closely.

INSERT, SEARCH, SORT

What is likely the most common operation?  READ ONLY, WRITE (MOSTLY), etc

Examine set of data structures to use.

Think about operational impact: IO, memory, etc.

http://www.cs.sunysb.edu/~algorith/video-lectures/2007/lecture5.pdf

Binary Search Tree superior in most operations.